Suppose that 5 J of work is needed to stretch a spring from its natural length of 36 cm to a length of 51 cm. (a) How much work is needed to stretch the spring from 41 cm to 46 …

Question

asked Apr 21, 2022 140k views

1 Answer

Tomaszbak · Answer 1 · 2022-04-25T13:03:48+0000

Answer:

a) 0.6 joules of work are needed to stretch the spring from 41 centimeters to 46 centimeters.

b) The spring must be 5.6 centimeters far from its natural length.

Explanation:

a) The work done to stretch the ideal spring from its natural length is defined by the following definition:

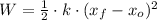$W = (1)/(2)\cdot k\cdot (x_(f)-x_(o))^(2)$ (1)

Where:

- Spring constant, measured in newtons.

x_(o) ,
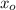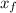x_(f) - Initial and final lengths of the spring, measured in meters.

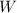- Work, measured in joules.

The spring constant is: (
$W = 5\,J$ ,
$x_(o) = 0.36\,m$ ,
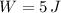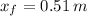$x_(f) = 0.51\,m$ )

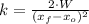
$k = (2\cdot W)/((x_(f)-x_(o))^(2))$

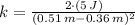
$k = (2\cdot (5\,J))/((0.51\,m-0.36\,m)^(2))$

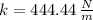
$k = 444.44\,(N)/(m)$

If we know that
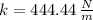$k = 444.44\,(N)/(m)$ ,
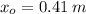$x_(o) = 0.41\,m$ and
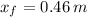$x_(f) = 0.46\,m$ , then the work needed is:

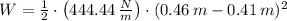
$W = (1)/(2)\cdot \left(444.44\,(N)/(m) \right)\cdot (0.46\,m-0.41\,m)^(2)$

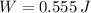
$W = 0.555\,J$

0.6 joules of work are needed to stretch the spring from 41 centimeters to 46 centimeters.

b) The elastic force of the ideal spring (
), measured in newtons, is defined by the following formula:

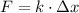$F = k\cdot \Delta x$ (2)

Where
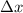$\Delta x$ is the linear difference from natural length, measured in meters.

If we know that
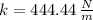$k = 444.44\,(N)/(m)$ and
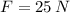$F = 25\,N$ , then the linear difference is:

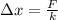
$\Delta x = (F)/(k)$

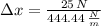
$\Delta x = (25\,N)/(444.44\,(N)/(m) )$

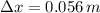
$\Delta x = 0.056\,m$

The spring must be 5.6 centimeters far from its natural length.