The first step for solving this problem is to multiply both sides of the bottom equation by -3.
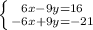
Add the two equations together.
6x - 9y - 6x + 9y = 16 - 21
Eliminate the opposites.
-9y + 9y = 16 - 21
Remember that the sum of two opposites equals 0,, so the equation becomes the following:
0 = 16 - 21
Calculate the difference on the right side of the equation.
0 = -5
This means that the statement

is false for any value of x and y. That means that the answer to your question is (x,y) ∈ ∅,, or no solution.
Let me know if you have any further questions.
:)