Question

Jackie plans to place a rectangular piece of art inside a rectangular frame. She considers a piece of art that is 0.5 meters long, 1.2 meters wide, and has a diagonal length of 1.3 meters. Which is true regarding the art piece? The art is rectangular because (0.5) squared + (1.2) squared = (1.3) squared. The art is rectangular because (1.2) squared minus (0.5) squared less-than (1.3) squared. The art is not rectangular because (0.5) squared + (1.2) squared not-equals (1.3) squared. The art is not rectangular because (0.5) squared + (1.2) squared greater-than (1.3) squared.

Answer 1

The art is rectangular because
`(0.5) ^2 + (1.2) ^2 = (1.3) ^2`

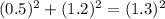
(0.5) squared + (1.2) squared = (1.3) squared

Explanation:

Given that the piece of art is rectangular in shape.

Length of piece of art = 0.5 meters

Width of piece of art = 1.2 meters

Kindly refer to the attached image in the answer area.

Two adjacent sides of a rectangle are given, the diagonal value can be found by using Pythagorean Theorem.

According to Pythagorean theorem:

`\text{Hypotenuse}^(2) = \text{Base}^(2) + \text{Perpendicular}^(2)`

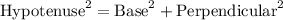
Here, Hypotenuse will be the diagonal of the rectangle.

Base and Perpendicular will be the two adjacent sides.

Therefore,

`Diagonal^2 = 0.5^2+0.12^2\\\Rightarrow Diagonal^2 = 0.25+1.44\\\Rightarrow Diagonal = √(1.69)\\\Rightarrow Diagonal = 1.3\ m`

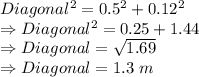
Therefore, the answer is:

The art is rectangular because
`(0.5) ^2 + (1.2) ^2 = (1.3) ^2`

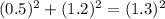
OR

(0.5) squared + (1.2) squared = (1.3) squared