Question

Which function grows at the fastest rate for increasing values of x?

h(x)=9.5x2

g(x)=2.5x

f(x)=8.5x+3

Answer 1

g(x)=2.5x
is your answere

Answer 2

h(x) grows in faster manner.

Explanation:

Let f(x) and g(x) be positive for large value of x

then we say f(x) grows faster than g(x) as x → ∞ if
`\lim_(x \to \infty) (f(x))/(g(x))`= +∞

Let f(x) and g(x) be positive for large value of x

then we say f(x) and g(x) grows with same rate if

as x → ∞ if
`\lim_(x \to \infty) (f(x))/(g(x))`= a finite non zero value.

Using above we can see g(x) and f(x) will grow slower than h(x) as

`\lim_(x \to \infty) (f(x))/(g(x))`

`\lim_(x \to \infty) (9.5x^2)/(2.5x))`

∞

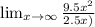
therefore h(x) grows in faster manner.