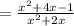Question

What is the difference x +5/ x +2 - x + 1/x ^2 + 2x?

Answer 1

The difference will be given by:
(x +5)/ (x +2) - (x + 1)/(x ^2 + 2x)
=(x +5)/ (x +2) - (x + 1)/[x (x + 2)]
the LCM is x(x+2)
thus the difference will be:
[x(x+5)-(x+1)]/(x (x + 2))
=[x^2+5x-x-1]/[x(x+2)]
=(x^2-4x-1)/[x(x+2)]

Answer:(x^2-4x-1)/[x(x+2)]

Answer 2

ANSWER
The difference is,


`\frac{ {x}^(2) + 4x - 1}{ {x}^(2) + 2x}`

Step-by-step explanation

To find the difference, we just have to simplify the expression.

The given expression is


`(x + 5)/(x + 2) - \frac{(x + 1)}{ {x}^(2) + 2x}`

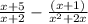
We factor the denominator of the second fraction to get,


`=(x + 5)/(x + 2) - ((x + 1))/( x( x+ 2))`

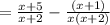
We can now see clearly that the LCM is


`x(x + 2)`

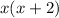
We collect LCM to get,


`=(x(x + 5) - (x + 1))/( x( x+ 2))`
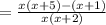
We now expand the bracket to obtain,


`=\frac{ {x}^(2) + 5x - x - 1}{ {x}^(2) + 2x}`

This gives us,


`=\frac{ {x}^(2) + 4x - 1}{ {x}^(2) + 2x}`