Question

The first-serve percentage of a tennis player in a match is normally distributed with a standard deviation of 4.3%. If a sample of 15 random matches of the player is taken, the mean first-serve percentage is found to be 26.4%. What is the margin of error of the sample mean? please provide explination

Answer 1

We shall use the z-table to solve for the margin of error. The formula for the margin of error is

`E=z_(\alpha /2)\cdot (\sigma )/(√(n))`

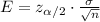
The value of z will be taken with the assumption that the significance level is 5%. So, α=0.025. Then
`z_(\alpha \:/2)=1.96`.

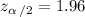
So, based from this, the margin of error is

`E=z_(\alpha /2)\cdot (\sigma )/(√(n))=1.96\cdot (0.043)/(√(15))=0.02`

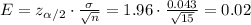
The margin of error is about 2%.