Question

Find the measure of
KM
KQ
LK
LR
NK
PM

Answer 1

Explanation:

Since, PN ≅ NR

RM ≅ MQ

PL ≅ LQ

QN, LR and PM are the medians and they intersect each other at point K which will be the centroid of ΔPQR.

By the property of centroid,

Point K will divide the medians in the ratio of 2 : 1

By this property,

PK : KM = 2 : 1

4 : KM = 2 : 1

`(4)/(KM)=(2)/(1)`

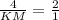
KM = 2

KQ =
`(2)/((2+1))(NQ)`

=
`(2)/(3)* 6`

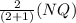
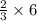
KQ = 4

LK : RK = 1 : 2

LK : 3 = 1 : 2

`(LK)/(3)=(1)/(2)`

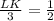
LK = 1.5

LR = LK + RK

= 1.5 + 3

LR = 4.5

NK =
`(1)/((2+1))(QN)`

=
`(1)/(3)(6)`

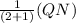
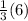
NK = 6

PM = PK + KM

PM = 4 + 2

PM = 6