Question

Ples help me find slant assemtotes

this one is different because it isn't a rational function



find the slant assemtotes of
`(y+1)^2=4xy`
the equation can be rewritten using the quadratic formula as
`y=2x-1 \pm √(x^2-x)`

ples find slant assemtotes and show all work
thx

Answer 1

which means the other asymptote is the line .

Answer 2

A polynomial asymptote is a function
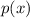
`p(x)` such that


`\displaystyle\lim_(x\to\pm\infty)(f(x)-p(x))=0`


`(y+1)^2=4xy\implies y(x)=2x-1\pm2√(x^2-x)`

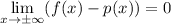
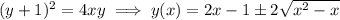
Since this equation defines a hyperbola, we expect the asymptotes to be lines of the form
`p(x)=ax+b`.

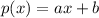
Ignore the negative root (we don't need it). If
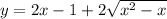
`y=2x-1+2√(x^2-x)`, then we want to find constants
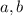
`a,b` such that


`\displaystyle\lim_(x\to\infty)(2x-1+2√(x^2-x)-ax-b)=0`

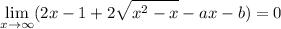
We have


`√(x^2-x)=√(x^2)√(1-\frac1x)`

`√(x^2-x)=|x|√(1-\frac1x)`

`√(x^2-x)=x√(1-\frac1x)`

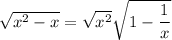
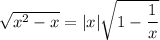
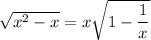
since
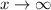
`x\to\infty` forces us to have
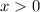
`x>0`. And as
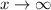
`x\to\infty`, the
`\frac1x` term is "negligible", so really
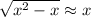
`√(x^2-x)\approx x`. We can then treat the limand like


`2x-1+2x-ax-b=(4-a)x-(b+1)`

which tells us that we would choose
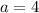
`a=4`. You might be tempted to think
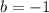
`b=-1`, but that won't be right, and that has to do with how we wrote off the "negligible" term. To find the actual value of
`b`, we have to solve for it in the following limit.


`\displaystyle\lim_(x\to\infty)(2x-1+2√(x^2-x)-4x-b)=0`


`\displaystyle\lim_(x\to\infty)(√(x^2-x)-x)=\frac{b+1}2`

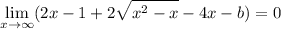
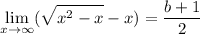
We write


`(√(x^2-x)-x)\cdot(√(x^2-x)+x)/(√(x^2-x)+x)=((x^2-x)-x^2)/(√(x^2-x)+x)=-\frac x{x√(1-\frac1x)+x}=-\frac1{√(1-\frac1x)+1}`

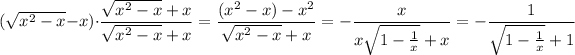
Now as
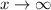
`x\to\infty`, we see this expression approaching
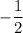
`-\frac12`, so that


`-\frac12=\frac{b+1}2\implies b=-2`

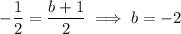
So one asymptote of the hyperbola is the line
`y=4x-2`.

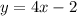
The other asymptote is obtained similarly by examining the limit as
`x\to-\infty`.


`\displaystyle\lim_(x\to-\infty)(2x-1+2√(x^2-x)-ax-b)=0`


`\displaystyle\lim_(x\to-\infty)(2x-2x√(1-\frac1x)-ax-(b+1))=0`

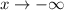
Reduce the "negligible" term to get


`\displaystyle\lim_(x\to-\infty)(-ax-(b+1))=0`

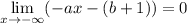
Now we take
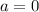
`a=0`, and again we're careful to not pick
`b=-1`.


`\displaystyle\lim_(x\to-\infty)(2x-1+2√(x^2-x)-b)=0`


`\displaystyle\lim_(x\to-\infty)(x+√(x^2-x))=\frac{b+1}2`


`(x+√(x^2-x))\cdot(x-√(x^2-x))/(x-√(x^2-x))=(x^2-(x^2-x))/(x-√(x^2-x))=\frac x{x-(-x)√(1-\frac1x)}=\frac1{1+√(1-\frac1x)}`

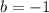
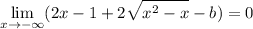
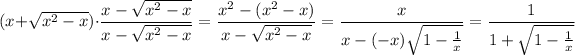
This time the limit is
`\frac12`, so


`\frac12=\frac{b+1}2\implies b=0`

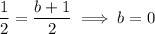
which means the other asymptote is the line
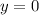
`y=0`.