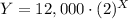Answer:
Explanation:
The exponential function is given by:
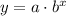
where,
a is the initial values and b is the growth factor.
As per the statement:
The initial number of bacteria in a culture is 12,000.
⇒Number of bacteria initially(a) = 12,000
It is also given that the culture doubles each day.
⇒ growth factor
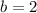
We have to find the exponential function to model the population Y of bacteria after X days.
By definition of exponential function:
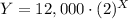
where, x represents the days and Y is the population after X days.
Therefore, an exponential function to model the population is,