Answer:
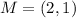
Explanation:
Represent the diagonals as:
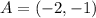

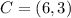
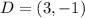
Required
Determine the coordinate of the intersection
To do this, we simply calculate the midpoint of AC or BD.
For AC:
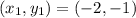
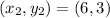
The midpoint is:
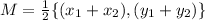
This gives:
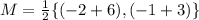
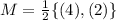

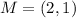
For BD:
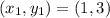
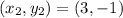
The midpoint is:
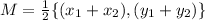
This gives:
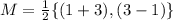
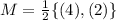

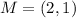
Notice the midpoints are the same:
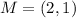
Hence, the coordinates of the intersection is (2,1)