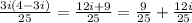Question

Simplify the expression The root of negative nine over the quantity of three minus two i plus the quantity of one plus five i.

Answer 1

This will be:
[√9]/[(3-2i)+(1+5i)]
simplifying the above we get:
√9/(3+1-2i+5i)
=√9/(4+3i)
rationalizing the denominator we get:
√9/(4-3i)×(4-3i)/(4-3i)
=[√9(4-3i)]/(16+9)
=[3(4-3i)]/25
=(12-9i)/25

Answer: (12-9i)/25

Answer 2

`(\sqrt-9)/([(3-2 i)+(1+5 i)])`

Remember these complex formulas

1.
`√(-1)=i`

2. (a + b i) + (c +d i)=(a +c) + i(b+d), i.e real part should be added or subtracted to real part and imaginary part should be added or subtracted to imaginary part.

3. ( a + b i)(a - bi)= a² + b²

4.
`i=√(-1),i^2=-1, i^3= -i, i^4=1`

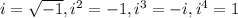
→So,
`√(-9)= √(-1) * √(9)= 3 i`

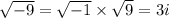
→3 - 2 i + 1 + 5 i= 4 + 3 i

→
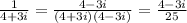`(1)/(4+3 i)=(4 - 3 i)/((4 + 3 i)(4 - 3 i))=\frac {4-3 i}{25}`→→Rationalizing the Denominator i.e complex number

→
`(\sqrt-9)/([(3-2 i)+(1+5 i)])`

=
`(3 i (4 - 3 i))/(25)=(12 i +9)/(25)=(9)/(25) +(12 i)/(25)`