Answer with explanation:
The average rate of change for function f(x) over the interval a ≤ x ≤ b is given by :-

So, the rate of change for function
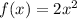 over the interval −3 ≤ x ≤ 4 :
over the interval −3 ≤ x ≤ 4 :

The rate of change for function
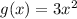 over the interval −3 ≤ x ≤ 4 :
over the interval −3 ≤ x ≤ 4 :
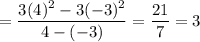
So, the rate of change for g(x) is greater than f(x) over the interval −3 ≤ x ≤ 4.