Answer:
x=-4,1,2+5i,2-5i
Explanation:
Given is an algebraic expression g(x) as product of two functions.
Hence solutions will be the combined solutions of two quadratic products

I expression can be factorised as
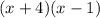
Hence one set of solutions are
x=-4,1
Next quadratic we cannot factorize
and hence use formulae
