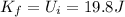Question

you stretch a spring by a distance of 0.3 m. the spring has a spring constant of 440 n/m. when you release the spring, it snaps back. what is the kinetic energy of the springs as it reaches its natural length?

Answer 1

19.8 J

Step-by-step explanation:

According to the law of conservation of energy, the total mechanical energy of the spring (sum of kinetic energy and elastic potential energy) must be conserved:

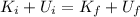`K_i + U_i = K_f + U_f` (1)

where we have

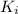`K_i` is the initial kinetic energy of the spring, which is zero because the spring starts from rest (2)

`U_i` is the elastic potential energy of the spring when it is fully stretched

`K_f` is the kinetic energy of the spring when it reaches the natural length

`U_f` is the elastic potential energy of the spring when it reaches its natural length, which is zero because the stretch in this case is zero (3)

So

`U_i = (1)/(2)k(\Delta x_i)^2`

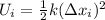
where

k = 440 N/m is the spring constant

`\Delta x_i = 0.3 m` is the initial stretching of the spring

Substituting,

`U_i = (1)/(2)(440)(0.3)^2=19.8 J`

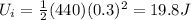
And so using eq.(1) and keeping in mind (2) and (3) we find

`K_f= U_i = 19.8 J`