Question

Wall-E the robot is resting when he randomly explodes into two pieces that fly off in opposite directions. His head has a mass of 0.75 kg and flies off to the right with a velocity of 75 m/s. If his body has a mass of 6.2 kg, what was its velocity after the explosion?

______________m/s (nearest hundredth)

Answer 1

The body flies off to the left at 9.1 m/s

Step-by-step explanation:

Law Of Conservation Of Linear Momentum

It states the total momentum of a system of bodies is conserved unless an external force is applied to it. The formula for the momentum of a body with mass m and speed v is

P=mv.

If we have a system of bodies, then the total momentum is the sum of the individual momentums:

`P=m_1v_1+m_2v_2+...+m_nv_n`

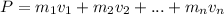
If a collision occurs and the velocities change to v', the final momentum is:

`P'=m_1v'_1+m_2v'_2+...+m_nv'_n`

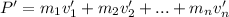
Since the total momentum is conserved, then:

P = P'

In a system of two masses, the equation simplifies to:

`m_1v_1+m_2v_2=m_1v'_1+m_2v'_2\qquad\qquad[1]`

Wall-E robot is initially at rest, its two parts together. His head has a mass of m1=0.75 kg and his body has a mass of m2=6.2 kg. Both parts have initial speeds of zero v1=v2=0.

After the explosion, his head flies off to the right at v1'=75 m/s. We are required to find the speed of his body v2'. Solving [1] for v2':

`\displaystyle v'_2=(m_1v_1+m_2v_2-m_1v'_1)/(m_2)`

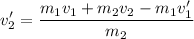
Substituting values:

`\displaystyle v'_2=(0.75*0+6.2*0-0.75*75)/(6.2)`

`\displaystyle v'_2=-9.1 \ m/s`

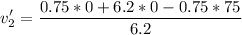
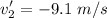
The body flies off to the left at 9.1 m/s