Answer:
7. 7.92 × 10−5
Step-by-step explanation:
Hello,
In this case, with the given pH, one could find the pOH:
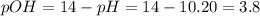
Thus, since barium hydroxide is completely dissolved in water based on:
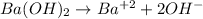
The concentration of hydroxyl ions is twice to that of the hydroxide (2:1 mole relationship). Therefore, by considering the relationship between the pOH and the concentration of hydroxyl we have:
![pOH=-log([OH]^-)\\](https://img.qammunity.org/2019/formulas/chemistry/college/zb60409on8hg5vpi4zxbigt89sbxyf6wgx.png)
![[OH]^-=10^(-3.8)=1.58x10^(-4)M](https://img.qammunity.org/2019/formulas/chemistry/college/labco5nta6fljztvuz3zok794bl3goxbse.png)
Finally, given the 1:2 mole ratio of barium hydroxide to hydroxyl ions, the concentration of barium hydroxide results:
![[Ba(OH)_2]=2*[OH^-]=(1)/(2) *1.58x10^(-4)M](https://img.qammunity.org/2019/formulas/chemistry/college/bapwe2975yfzzywh14qgfb6puxynxozoyg.png)
![[Ba(OH)_2]=7.92x10^(-5)M](https://img.qammunity.org/2019/formulas/chemistry/college/k4hkzt6hgx4t4q9tx3bsn1c267idgbk7aj.png)
Thus, the answer is 7. 7.92 × 10−5.
Regards.