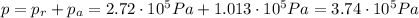Question

Calculate the absolute pressure at the bottom of a freshwater lake at a point whose depth is 27.8 m. assume the density of the water is 1.00 103 kg/m3 and the air above is at a pressure of 101.3 kpa.

Answer 1

The relative pressure at the bottom of the lake is given by

`p_r = \rho g h`
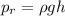
where

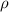
`\rho` is the water density
g is the gravitational acceleration
h is the depth at which the pressure is measured

At the bottom of the lake, h=27.8 m, so the relative pressure is

`p_r = (1\cdot 10^3 kg/m^3)(9.81 m/s^2)(27.8 m)=2.72 \cdot 10^5 Pa`

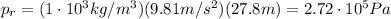
To find the absolute pressure, we must add the atmospheric pressure,
`p_a`, to this value:

`p=p_r + p_a =2.72 \cdot 10^5 Pa + 1.013 \cdot 10^5 Pa =3.74 \cdot 10^5 Pa`