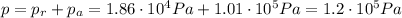Question

Determine the absolute pressure on the bottom of a swimming pool 30.0 m by 9.0 m whose uniform depth is 1.9 m . express your answer using two significant figures.

Answer 1

The relative pressure at the bottom of a column of fluid is given by

`p_r = \rho g h`
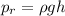
where

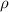
`\rho` is the fluid density
g is the gravitational acceleration
h is the height of the column of fluid

At the bottom of the swimming pool, h=1.9 m, and the water density is

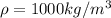
`\rho = 1000 kg/m^3`, therefore the relative pressure is

`p_r = (1000 kg/m^3)(9.81 m/s^2)(1.9 m)=1.86 \cdot 10^4 Pa`

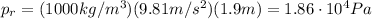
To find the absolute pressure, we must add to this the atmospheric pressure,
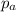
`p_a`:

`p= p_r + p_a= 1.86 \cdot 10^4 Pa + 1.01 \cdot 10^5 Pa =1.2 \cdot 10^5 Pa`