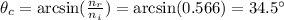Question

A ray of light traveling in air strikes the surface of a liquid. if the angle of incidence is 29.7◦ and the angle of refraction is 16.3◦ , find the critical angle for light traveling from the liquid back into the air. answer in units of ◦

Answer 1

When light moves from a medium with higher refractive index to a medium with lower refractive index, the critical angle is the angle above which there is no refracted ray, and it is given by:

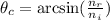
`\theta_c = \arcsin ( (n_r)/(n_i) )` (2)
where
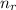
`n_r` is the refractive index of the second medium and
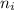
`n_i` is the refractive index of the first medium.

We can find the ratio
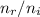
`n_r / n_i` by using Snell's law:

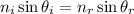
`n_i \sin \theta_i = n_r \sin \theta_r` (1)
where

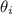
`\theta_i` is the angle of incidence

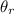
`\theta_r` is the angle of refraction

By using the data of the problem and re-arranging (1), we find

`(n_r)/(n_i) = (\sin \theta_i)/(\sin \theta_r) = (\sin 16.3^(\circ))/(\sin 29.7^(\circ)) =0.566`

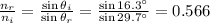
and if we use eq.(2) we can now find the value of the critical angle:

`\theta_c = \arcsin ( (n_r)/(n_i) ) = \arcsin (0.566) = 34.5^(\circ)`