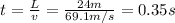Question

I would love to stretch a wire from our house to the Shop so I can 'call' my husband in for meals. The wire could be tightened to have a tension of 240N and a m/L 'weight' of 0.05kg/L. How long would it take for my pulse wave to travel to the Shop (24m) to ring a bell to indicate dinner time.

Answer 1

Note: I'm not sure what do you mean by "weight 0.05 kg/L". I assume it means the mass per unit of length, so it should be "0.05 kg/m".

Solution:
The fundamental frequency in a standing wave is given by

`f= (1)/(2L) \sqrt{ (T)/(m/L) }`
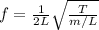
where L is the length of the string, T the tension and m its mass. If we plug the data of the problem into the equation, we find

`f= (1)/(2 \cdot 24 m) \sqrt{ (240 N)/(0.05 kg/m) }=1.44 Hz`

The wavelength of the standing wave is instead twice the length of the string:

`\lambda=2 L= 2 \cdot 24 m=48 m`

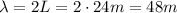
So the speed of the wave is

`v=\lambda f = (48 m)(1.44 Hz)=69.1 m/s`

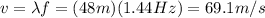
And the time the pulse takes to reach the shop is the distance covered divided by the speed:

`t= (L)/(v)= (24 m)/(69.1 m/s)=0.35 s`