Answer:
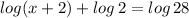 is required lograthmic equation.
is required lograthmic equation.
Explanation:
Given: Given equation, x - 4 = 2³
To find: Logarithmic function whose solution is same as given equation.
First we find the solution of given Equation.
consider,
x - 4 = 2³
x - 4 = 8 ( ∵ 2³ = 2×2×2 = 8 )
x = 8 + 4 ( Transposing 4 to RHS )
x = 12
Now we find the logarithmic equation whose solution is also x = 12.
( There exist many such equations )
Lets say one of them is,
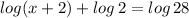
Now we find its solution to check if it is same or not.
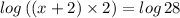 (using lograthmic rule,
(using lograthmic rule,
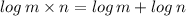 )
)
⇒ 2 × ( x + 2 ) = 28 (using lograthmic rule,
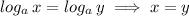 )
)
⇒ 2x + 4 = 28
⇒ 2x = 28 - 4 (transposing 4 to RHS)
⇒ 2x = 24 (transposing 2 to RHS)
⇒
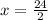
⇒ x = 12
Therefore,
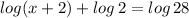 is required lograthmic equation.
is required lograthmic equation.