Question

Use Cavalieri’s Principle to calculate the exact volume of an oblique cylinder with a radius of 5 inches and a height of 16 inches.

Answer 1

V= (pi)r^29(h)
V= (pi) 25(16)

V= 400(pi) in^3

Answer 2

`V=400{\pi} in^3`

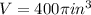
Explanation:

Cavalieri’s Principle: If in two solids of equal altitude, the sections made by planes parallel to and at the same distance from their respective bases are always equal, then the volumes of the two solids are equal.

Thus, we are given that the radius of the cylinder is 5 inches and height is 16 inches, therefore volume of oblique cylinder is given as:

`V={\pi}r^2h`

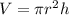
Substituting the given values,, we have

`V={\pi}(5)^2(16)`

`V={\pi}(25)(16)`

`V=400{\pi} in^3`

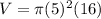
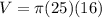
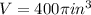
Thus, the volume of the oblique cylinder is 400π cubic inches.