Answer: The probability of hitting an odd number three times is
 times more than the probability of hitting an even number 3 times.
times more than the probability of hitting an even number 3 times.
Explanation:
From the given picture , the total total number of sections in the spinner = 5
Sections having Odd numbers = 3
Sections having Even numbers =2
We know that ,
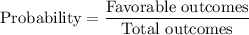
So , probability of hitting an odd number =

Probability of hitting an even number =

Since all events are independent of each other ,
So , probability of hitting an odd number three times =
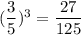
Probability of hitting an even number three times =
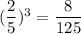
Divide
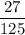 by
by
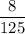 , we get
, we get
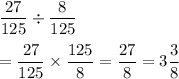
Hence, the probability of hitting an odd number three times is
 times more than the probability of hitting an even number 3 times.
times more than the probability of hitting an even number 3 times.