Question

The dot product of u with itself is 12. what is the magnitude of u?

Answer 1

let's say u = <a,b>.

we know it's dot product is 12, thus


`\bf \ \textless \ a,b\ \textgreater \ \cdot \ \textless \ a,b\ \textgreater \ \implies (a\cdot a)+(b\cdot b)\implies \boxed{a^2+b^2=12}\\\\ -------------------------------\\\\ ||\ \textless \ a,b\ \textgreater \ ||=√(a^2+b^2)\implies \sqrt{\boxed{12}}`

Answer 2

Answer: The magnitude of the vector u is √12 units.

Step-by-step explanation: Given that the dot product of a vector u with itself is 12.

We are to find the magnitude of the vector u.

Let <a, b> represents the vector u.

That is, u = <a, b>

Then, according to the given information, we have

`u.u=12\\\\\Rightarrow <a, b>.<a, b>=12\\\\\Rightarrow a^2+b^2=12\\\\\Rightarrow √(a^2+b^2)=√(12)\\\\\Rightarrow |u|=√(12).`

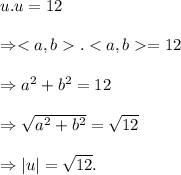
Thus, the magnitude of the vector u is √12 units.