Question

How does the graph of y=1/2(x+4)^2compare to the graph of y=(x-1)^2 -3?

Answer 1

`\bf ~~~~~~~~~~~~\textit{function transformations} \\\\\\ % templates f(x)= A( Bx+ C)+ D \\\\ ~~~~y= A( Bx+ C)+ D \\\\ f(x)= A√( Bx+ C)+ D \\\\ f(x)= A(\mathbb{R})^( Bx+ C)+ D \\\\ f(x)= A sin\left( B x+ C \right)+ D \\\\ --------------------`


`\bf \bullet \textit{ stretches or shrinks horizontally by } A\cdot B\\\\ \bullet \textit{ flips it upside-down if } A\textit{ is negative}\\ ~~~~~~\textit{reflection over the x-axis} \\\\ \bullet \textit{ flips it sideways if } B\textit{ is negative}`


`\bf ~~~~~~\textit{reflection over the y-axis} \\\\ \bullet \textit{ horizontal shift by }( C)/( B)\\ ~~~~~~if\ ( C)/( B)\textit{ is negative, to the right}\\\\ ~~~~~~if\ ( C)/( B)\textit{ is positive, to the left}\\\\ \bullet \textit{ vertical shift by } D\\ ~~~~~~if\ D\textit{ is negative, downwards}\\\\ ~~~~~~if\ D\textit{ is positive, upwards}\\\\ \bullet \textit{ period of }(2\pi )/( B)`

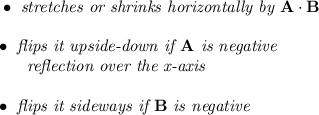
and now with that template in mind,

bearing in mind the parent function for both is just y = x², or y = 1(1x + 0)² + 0.


`\bf y=\stackrel{A}{\cfrac{1}{2}}(x\stackrel{C}{+4})^2`

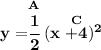
is x² but expanded by twice as much vertically, and has a horizontal shift of +4, namely 4 units to the left.

y=(x-1)² - 3

is just x² but with a horizontal shfit of -1, namely 1 unit to the right, and a vertical shift of -3, namely 3 units down.