Given
volume of the sphere is 500/3 π cubic units.
Find the value of x .
To proof
FORMULA

where r is the radius of sphere.
As given in question
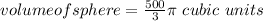
now as shown in the diagram
The radius of the sphere is x.
put all the values in the above equation
we get
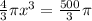
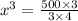
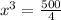

![x = \sqrt[3]{125}](https://img.qammunity.org/2019/formulas/mathematics/high-school/gdde7qyqj8u4pwjnekycuu4fpqepisojl7.png)
x =5
Thus the value of 5 units.
Hence proved