Question

Find the value of sin2a, if tana=-12/5 in the fourth quadrant

Answer 1

`\tan a=-\frac{12}5`

Recall the following identities:


`1+\tan^2a=\sec^2a=\frac1{\cos^2a}`

`\cos^2a=\frac{1+\cos2a}a`

from which we get


`1+\left(-\frac{12}5\right)^2=\frac1{\cos^2a}`

`\implies\cos^2a=(25)/(169)`

Since
`a` is in the fourth quadrant
`\left(\frac{3\pi}2<a<2\pi\right)` we know that
`\cos a` should be positive, so when we take the square root here, we should take the positive root.


`\implies\cos a=\sqrt{(25)/(169)}=\frac5{13}`

Now recall that


`\cos^2a+\sin^2a=1`

and since
`a` is in the fourth quadrant, we expect
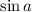
`\sin a` to be negative. So,


`\sin^2a=1-\cos^2a=(144)/(169)\implies\sin a=-\sqrt{(144)/(169)}=-(12)/(13)`

One final identity:


`\sin2a=2\sin a\cos a`

from which we get


`\sin2a=2\cdot\left(-(12)/(13)\right)\cdot\frac5{13}=-(120)/(169)`