Answer:
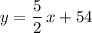 .
.
(Equivalently,
 .)
.)
Explanation:
Rewrite the equation of the line
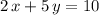 in the slope-intercept form
in the slope-intercept form
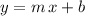 to find the slope
to find the slope
 .
.
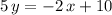 .
.
 .
.
Therefore, the slope of the line
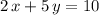 is
is
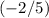 .
.
Let
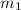 and
and
 denote the slope of two lines on a cartesian plane. If these two lines are perpendicular to one another, then
denote the slope of two lines on a cartesian plane. If these two lines are perpendicular to one another, then
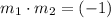 .
.
In this question, the slope of the first line was already found
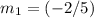 . Solve
. Solve
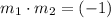 for the slope
for the slope
 of the unknown line:
of the unknown line:
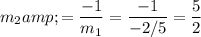 .
.
The following information are thus available for the requested line:
- The slope of this line is
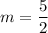 .
. - This line contains the point
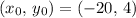 .
.
Hence, the point-slope form
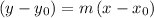 would be a possible choice for the equation of this line:
would be a possible choice for the equation of this line:
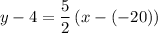 .
.
Simplify to obtain the slope-intercept form equation of this line:
 .
.
Equivalently:
 .
.