Question

X + 8 = −x2 + 4x + 12

Answer 1

The answer is x=−1 or x=4.

Combine like terms and divide!

Answer 2

you bring all xs on one side then you solve as quadratic analysis.

`x + 8 + {x}^(2) - 4x - 12 = 0`

`{x}^(2) - 3x - 4 = 0`
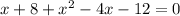
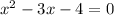
so you can simplify into

`(x + 1)(x - 4) = 0`
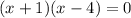
*Note that here 4 took the negative sign and 1 took the positive sign, as you want to numbers that if multiplied will give -4 and when added will give -3, and these are (-4 and 1)*

so now you can simply say that, for the equation to equal 0, x should be -1 or 4.
You can always substitute to make sure of your calculations.

Hope this helps.