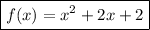Answer:
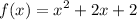
Explanation:
System Of Linear Equations
In this problem, we'll need to solve a 3x3 system of linear equations because we have three unknowns and three conditions.
We are required to find the equation of the quadratic function that passes through the points (-1, 1), (1, 5), and (2,10)
The general quadratic function can be written as
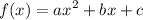
We need to find the values of a,b, and c. Let's use the first condition, i.e. f(-1)=1
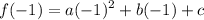
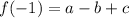
![\displaystyle a-b+c=1.....[eq\ 1]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/aeig5lisxt6b9n1ijz0x582l9kr9t5lggo.png)
Now we use the second condition f(1)=5


![\displaystyle a+b+c=5.......[eq\ 2]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/i2kkyabkcykr8zsivgiffa75uu7rqzbbkf.png)
Finally, we use the third condition f(2)=10
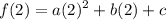
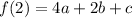
![\displaystyle 4a+2b+c=10....[eq\ 3]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/scvee0i014rv87adfrmzugx7i82fp63gee.png)
We put together eq 1, eq 2, and eq 3 to form the system
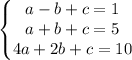
Adding the first two equations we have

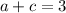
And also
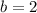
Using the above equation and the value of b in the third equation, we have

Subtracting the first equation from the second
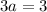
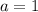
And therefore
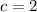
Now we have all the values, the quadratic function is