Question

Which expression is a cube root of -1+i√3?

A. ^3√2(cos120 + i sin 120)
B. ^3√4(cos320 + i sin 320)
C. ^3√2(cos40 + i sin 40)
D. ^3√4(cos280 + i sin 280)

Answer 1

The correct option is C.

Explanation:

Root Of Complex Numbers

If a complex number is expressed in polar form as

`Z=(r,\theta)`

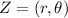
Then the cubic roots of Z are

`\displaystyle Z_1=\left(\sqrt[3]{r},(\theta)/(3)\right)`

`\displaystyle Z_2=\left(\sqrt[3]{r},(\theta)/(3)+120^o\right)`

`\displaystyle Z_3=\left(\sqrt[3]{r},(\theta)/(3)+240^o\right)`

We are given the complex number in rectangular components

`Z=-1+i√(3)`

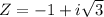
Converting to polar form

`r=\sqrt{(-1)^2+(√(3))^2}=2`

`\displaystyle tan\theta=(√(3))/(-1)=-√(3)`

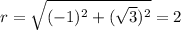
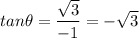
It's located in the second quadrant, so

`\theta=120^o`

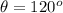
The number if polar form is

`Z=(2,120^o)`

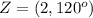
Its cubic roots are

`\displaystyle Z_1=\left(\sqrt[3]{2},(120^o)/(3)\right)=\left(\sqrt[3]{2},40^o\right)`

`\displaystyle Z_2=\left(\sqrt[3]{2},40^o+120^o\right)=\left(\sqrt[3]{2},160^o\right)`

`\displaystyle Z_3=\left(\sqrt[3]{2},40^o+240^o\right)=\left(\sqrt[3]{2},280^o\right)`

Converting the first solution to rectangular coordinates

`z_1=\sqrt[3]{2}(\ cos40^o+i\ sin40^o)`

The correct option is C.