Question

A 20 cannon ball is loaded into 700 cannon on wheels. After the explosion, the "muzzle" velocity of the cannon ball is 400 meters/second toward the east. What is the "recoil" velocity of cannon on wheels as it reacts in the opposite direction?

Answer 1

vcannon = 11.42 [m/s]

Step-by-step explanation:

To solve this problem we must use the principle of conservation of linear momentum which tells us that the momentum of the cannon ball is conserved before and after shooting.

This is at the time of the shot we have two movements, that of the cannon ball moving to the East, while the cannon moves to the left due to the reaction caused by the explosion.

`0 = -(m_(cannon)*v_(cannon))+(m_(cannonball)*v_(cannonball))\\`

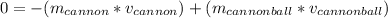
where:

mcannon = mass of the cannon = 700 [kg]

vcannon = velocity of the cannon [m/s]

mcannonball = 20 [kg]

vcannonball = 400 [m/s]

Now replacing:

`0=-(700*v_(cannon))+(20*400)\\v_(cannon)=11.42 [m/s]`