Question

A photograph has a length that is 3 inches longer than its width, x. So its area is given by the expression x(x+3) square inches. If the area of the photograph is 70 square inches, what is the length of the photograph?

The length of the photograph is_________inches?

Answer 1

The length of the photograph is 10 inches.

Step-by-step explanation:

Given, Width of a photograph is x.

Length of the photograph is 3 inches longer than its width. i.e. x + 3.

Area of the photograph = x(x+3)

If its area is 70 square inches, then

x(x+3)=70

`x^2 + 3x = 70`

`x^2 + 3x-70 = 0`

`x^2 - 7x + 10x-70 = 0`

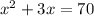
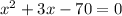
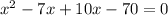
x(x-7)+10(x-7)=0

(x+10)(x-7) =0

x+10=0; x-7 = 0

x = -10 and x = 7

Width of the photograph must not be in negative value. So, we can ignore –10.

Therefore, width of the photograph, x = 7 inches.

Now, the length of the photograph = 7 + 3 = 10 inches.

Thus, the required length of the photograph is 10 inches.