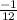Answer:
x= 0 ,
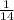 ,
,
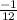
Explanation:
Given, equation is
![\sqrt[3]{15x-1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/19samxqi8zvhr6esau2zya5kd2wt7wlbtt.png) +
+
![\sqrt[3]{13x+1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pm5l682dijiaz5ovsriqseq1v5xe9iksr0.png) =
=
![4\sqrt[3]{x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/spsi8hitse7ao80ctfbj8hrxm34vrbgvhc.png) . →→→ (1)
. →→→ (1)
Now, by cubing the equation on both sides, we get
(
![\sqrt[3]{15x-1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/19samxqi8zvhr6esau2zya5kd2wt7wlbtt.png) +
+
![\sqrt[3]{13x+1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pm5l682dijiaz5ovsriqseq1v5xe9iksr0.png) )³ = (
)³ = (
![4\sqrt[3]{x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/spsi8hitse7ao80ctfbj8hrxm34vrbgvhc.png) )³
)³
⇒ (15x-1) + (13x+1) + 3×
![\sqrt[3]{15x-1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/19samxqi8zvhr6esau2zya5kd2wt7wlbtt.png) ×
×
![\sqrt[3]{13x+1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pm5l682dijiaz5ovsriqseq1v5xe9iksr0.png) (
(
![\sqrt[3]{15x-1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/19samxqi8zvhr6esau2zya5kd2wt7wlbtt.png) +
+
![\sqrt[3]{13x+1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pm5l682dijiaz5ovsriqseq1v5xe9iksr0.png) ) = 64 x.
) = 64 x.
⇒ 28x + 3×
![\sqrt[3]{15x-1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/19samxqi8zvhr6esau2zya5kd2wt7wlbtt.png) ×
×
![\sqrt[3]{13x+1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pm5l682dijiaz5ovsriqseq1v5xe9iksr0.png) (
(
![4\sqrt[3]{x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/spsi8hitse7ao80ctfbj8hrxm34vrbgvhc.png) ) = 64x.
) = 64x.
(since from (1),
![\sqrt[3]{15x-1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/19samxqi8zvhr6esau2zya5kd2wt7wlbtt.png) +
+
![\sqrt[3]{13x+1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pm5l682dijiaz5ovsriqseq1v5xe9iksr0.png) =
=
![4\sqrt[3]{x}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/spsi8hitse7ao80ctfbj8hrxm34vrbgvhc.png) )
)
⇒ 12×
![\sqrt[3]{15x-1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/19samxqi8zvhr6esau2zya5kd2wt7wlbtt.png) ×
×
![\sqrt[3]{13x+1}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/pm5l682dijiaz5ovsriqseq1v5xe9iksr0.png) (
(
![\sqrt[3]{x}](https://img.qammunity.org/2020/formulas/mathematics/high-school/adp5h6zbpgyn5rixh96ki4nbf91jilhd94.png) )= 36x.
)= 36x.
⇒ 3x =
![\sqrt[3]{(15x-1)(13+1)(x)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x74yfi5mbh25zqla3jegoggtb3cjcemoib.png) .
.
Now, once again cubing on both sides, we get
(3x)³ = (
![\sqrt[3]{(15x-1)(13+1)(x)}](https://img.qammunity.org/2020/formulas/mathematics/middle-school/x74yfi5mbh25zqla3jegoggtb3cjcemoib.png) )³.
)³.
⇒ 27x³ = (15x-1)(13x+1)(x).
⇒ 27x³ = 195x³ + 2x² - x
⇒ 168x³ + 2x² - x = 0
⇒ x(168x² + 2x -1) = 0
⇒ by, solving the equation we get ,
x = 0 ; x =
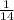 ; x =
; x =
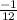
therefore, solution is x= 0 ,
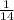 ,
,