Question

Find (fog)(2) and (f+g)(2) when f(x) =1/x and g(x) =4x+9

Answer 1

`( f o g)(2) = (1)/(17)`

`(f + g)(2) = (35)/(2)`

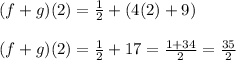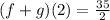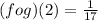
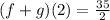
Solution:

Given that:

`f(x) = (1)/(x)\\\\g(x) = 4x + 9`

To find: (fog)(2) and (f + g)(2)

By composite function,

( f o g)(x) = f (g(x))

Substitute g(x) = 4x + 9 in above formula,

( f o g)(x) = f(4x + 9)

To find (fog)(2) substitute x = 2 in above formula

( f o g)(2) = f(4(2) + 9)

( f o g)(2) = f(8 + 9) = f(17)

We know that
`f(x) = (1)/(x)`

`( f o g)(2) = f(17) = (1)/(17)`

`( f o g)(2) = (1)/(17)`

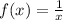
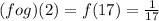
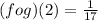
To find (f + g)(2)

We know that,

(f + g)(x) = f (x) + g(x)

Therefore,

(f + g)(2) = f(2) + g(2)

Substitute x = 2 in f(x) and g(x)

`(f + g)(2) = (1)/(2) + (4(2) + 9)\\\\(f + g)(2) = (1)/(2) + 17 = (1+34)/(2) = (35)/(2)`

`(f + g)(2) = (35)/(2)`