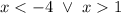Answer:
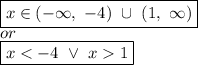
Explanation:
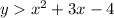
STEP 1:
Find the zeros of a parabola.

STEP 2:
Sketch a parabola.
The coefficient at x² is 1. It's a positive number, therefore the parabola is open up.
(attachment #1)
STEP 3:
Mark the regions where the graph is above the axis.
(attachment #2)
STEP 4:
Read selected intervals
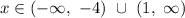
or