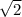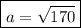Question

A rectangle with sides 12 cm and 14 cm has the same diagonal as a square.

What is the length of the side of the square.
Give your answer as a surd.​

Answer 1

`a=√(170)`

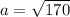
Explanation:

Diagonal of a Square

Given a square of length side a, the length of the diagonal is

`D=√(2)a`

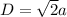
The diagonal of a rectangle of sides x and y is

`D=√(x^2+y^2)`

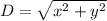
The sides have lengths 12 cm and 14 cm, the diagonal is

`D=√(12^2+14^2)`

`D=√(340)`

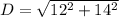
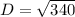
Since this value is the same of the diagonal of certain square, we can say

`√(2)a=√(340)`

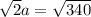
Dividing by
`√(2)`

`\boxed{a=√(170)}`