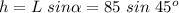Question

An 85-foot rope from the top of a tree house to the ground forms a 45 degree angle of elevation from the ground. How high is the top of the tree house in feet?

Answer 1

`\boxed{h=60.1\ ft }`

Explanation:

Right Triangles

They have a right angle (90°) and a longer side called the hypotenuse opposite to the right angle. The legs and the hyponetuse form two angles that must sum 90°, and they comply:

`\displaystyle sin\ \alpha=\frac {opp-leg}{hypotenuse}`

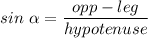
Where opp-leg is the opposite leg to
`\alpha.`

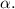
The rope from the top of a tree house is 85-foot long. It's the hypotenuse (L) of the triangle it forms with the ground and the tree. The angle of 45° is opposite to the height of the tree (h).

`\displaystyle sin\ \alpha=\frac {h}{L}`

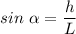
We can solve for h

`h=L\ sin\alpha =85\ sin\ 45^o`

`\boxed{h=60.1\ ft }`