Answer:
The trigonometrical expression is sin² A + sin A - 2 cos A - 2 cos A × sin A = 0
Explanation:
Given Trigonometrical function as :
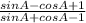 = 2 (1 + cosec A)
= 2 (1 + cosec A)
Or,
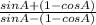 = 2 (1 + cosec A)
= 2 (1 + cosec A)
, Now, rationalizing
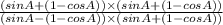 = 2 (1 + cosec A)
= 2 (1 + cosec A)
Or,
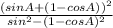 = 2 ( 1 +
= 2 ( 1 +
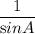
Or,
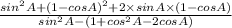 = 2 (
= 2 (
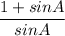
Or,
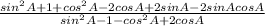 = 2 (
= 2 (
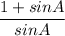
Or,
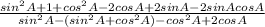 = 2 (
= 2 (
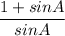
Or,
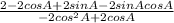 = 2 (
= 2 (
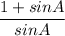
Or,
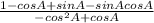 = 2 (
= 2 (
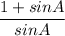
Or,
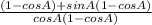 = 2 (
= 2 (
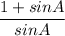
Or,
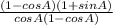 = 2 (
= 2 (
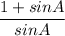
Or,
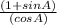 = 2 (
= 2 (
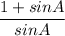
Or, sin A + sin² A = 2 cos A (1 + sin A)
Or, sin A + sin² A = 2 cos A + 2 cos A × sin A
Or, sin² A + sin A - 2 cos A - 2 cos A × sin A = 0
So,The trigonometrical expression is sin² A + sin A - 2 cos A - 2 cos A × sin A = 0 Answer