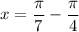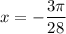Question

If cosxcos(pi/7)+sinxsin(pi/7)=root2/2

Answer 1

`\displaystyle x=(11\pi)/(28)`

`\displaystyle x=-(3\pi)/(28)`

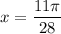
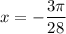
Explanation:

Cosine Of A Sum Of Angles

The cosine of the sum of angles can be expressed in terms of the individual angles as follows

`cos(a+b)=cos\ a\ cos\ b-sin\ a\ sin\ b`

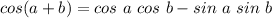
The cosine of the subtraction of angles is

`cos(a-b)=cos\ a\ cos\ b+sin\ a\ sin\ b`

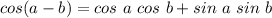
Since we have

`\displaystyle cosx\ cos((\pi)/(7))+sinx\ sin((\pi)/(7))=(√(2))/(2)`

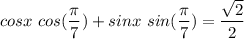
We can see it's equivalent to the cosine of the subtraction of angles, thus

`\displaystyle cosx\ cos((\pi)/(7))+sinx\ sin((\pi)/(7))=cos(x-(\pi)/(7))`

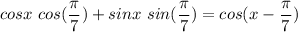
Completing the equation we have

`\displaystyle cos(x-(\pi)/(7))=(√(2))/(2)`

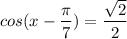
We know

`\displaystyle cos\ (\pi)/(4)=(√(2))/(2)`

And also

`\displaystyle cos\ (-(\pi)/(4))=(√(2))/(2)`

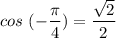
So we have two possible solutions

`\displaystyle x-(\pi)/(7)=(\pi)/(4)`

`\displaystyle x-(\pi)/(7)=-(\pi)/(4)`

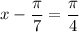
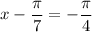
Thus, the first solution is

`\displaystyle x=(\pi)/(7)+(\pi)/(4)`

`\displaystyle x=(11\pi)/(28)`

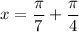
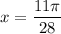
And the second solution is

`\displaystyle x=(\pi)/(7)-(\pi)/(4)`

`\displaystyle x=-(3\pi)/(28)`