Answer:
f(x) =
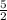 x
x
Explanation:
The first thing we need to find is the slope of the line able to pass through the given two points. Right now we have y = mx + b (linear function equation) and we need to find m.
- Using the slope formula or
 and plugging in the given points' x and y values:
and plugging in the given points' x and y values:
 =
=
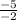 =
=
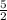
- The slope of the line is that for every 5 units the line goes upwards, it goes 2 units to the right.
Our equation is now y =
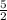 x + b. If you were in need of it, b gives the line's y-intercept, the place where it hits the y-axis. In this case you do not need b because the only specified conditions in the problem are the units the line hits.
x + b. If you were in need of it, b gives the line's y-intercept, the place where it hits the y-axis. In this case you do not need b because the only specified conditions in the problem are the units the line hits.
Our final equation is:
f(x) =
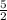 x
x