Question

If y ?-x, and every Xi is i i d with a chi-squared distribution with 14 degrees of freedom, find the MGF of Y M(t) = What is the distribution of Y? Select all that apply. There may be more than one correct answer A.chi squared(df 105) B. exponential(A 105 C. garnma(a = 2, ? = 210) D.gamma(a 1, 1/210) erponential(? = 210) F. chi-squared(df-210) G. gamma(a 105,B-2) H. garn ma(a-1, ?-1/105) I. None of the above

Answer 1

F. chi-squared(df-210)

Explanation:

The Chi Square distribution is the distribution of the sum of squared standard normal deviates .

We have independent and identically distributed random chi square variables, each one with 14 degrees of freedom
`X_i \sim \chi^2_(14)` for
`i=1,2,....,15`. And let Y the random variable defined as :

`Y= \sum_(i=1)^(15)X_i`

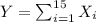
We have a thorem that says that the distribution of Y is given by:
`Y\sim \chi^2_(14+14+......+14=15*14=210)`

Proof

We need to find first the moment generating function for the random variable Y like this:

`M_Y (t) =\prod_(i=1)^(15)M_(X_i (t))`

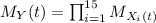
And the productory is satisfied because we have independent random variables. The moment generating function for a chi square distribution with r1 degrees of freedom is given by:

`M_X (t) =(1-2t)^{-(r_1)/(2)}`

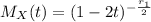
And replacing for each of the 15 distributions we got :

`M_Y (t) =\prod_(i=1)^(15)M_(X_i (t))= (1-2t)^{-(14)/(2)} (1-2t)^{-(14)/(2)}..... (1-2t)^{-(14)/(2)}`

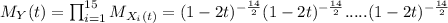
And using properties of algebra we got this:

`M_Y (t) = (1-2t)^-{(14+14+.....+14)/(2)}, t <1/2`

And we can see that the moment generating function represent a chi square distribution with 14*15=210 degrees of freedom.

So then the correct option is given by:

F. chi-squared(df-210)