Question

The mass of a star is 1.61·1031 kg and its angular velocity is 1.60E-7 rad/s. Find its new angular velocity if the diameter suddenly shrinks to 0.29 times its present size. Assume a uniform mass distribution before and after. Icm for a solid sphere of uniform density is 2/5 mr2. 1.90×10-6 rad/s

Answer 1

ω₂ = 1.9025 x 10⁻⁶ rad/s

Step-by-step explanation:

given,

mass of star = 1.61 x 10³¹ kg

angular velocity = 1.60 x 10⁻⁷ rad/s

diameter suddenly shrinks = 0.29 x present size

r₂ = 0.29 r₁

using conservation of angular momentum

I₁ ω₁ = I₂ ω₂

`((2)/(5)mr_1^2)\omega_1=((2)/(5)mr2^2)\omega_2`

`r_1^2* \omega_1=r_2^2* \omega_2`

`r_1^2* 1.60* 10^(-7)=(0.29r_1)^2* \omega_2`

`1.60* 10^(-7)=0.0841* \omega_2`

`\omega_2=(1.60* 10^(-7))/(0.0841)`

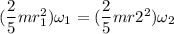
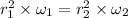
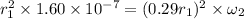
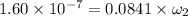
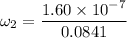
ω₂ = 1.9025 x 10⁻⁶ rad/s