Answer:
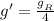
Step-by-step explanation:
Given:
- gravitational field strength of moon at a distance R from its center,
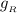
- Distance of the satellite from the center of the moon,
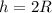
Now as we know that the value of gravity of any heavenly body is at height h is given as:
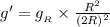
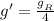
∴The gravitational field strength will become one-fourth of what it is at the surface of the moon.