Question

Calculate the work performed by an ideal Carnot engine as a cold brick warms from 150 K to the temperature of the environment, which is 300 K. (Use 300 K as the temperature of the hot reservoir of the engine). The heat capacity of the brick is C = 1 kJ/K.

Answer 1

To solve this problem, apply the concepts related to the calculation of the work performed according to the temperature change (in an ideal Carnot cycle), for which you have to:

`W = \int\limit_(T_c)^(T_H) C (1-(T_H)/(T))`

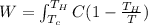
Where,

C = Heat capacity of the Brick

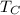`T_C`= Cold Temperature

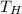`T_H` = Hot Temperature

Integrating,

`W = C (T_H-T_C)- T_H C ln ((T_H)/(T_C))`

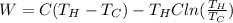
Our values are given as

`T_H= 300K`

`T_C = 150K`

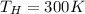
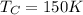
Replacing,

`W = (1) (300-150)-300(1)ln(2)`

`W = 150-300ln2`

`W = -57.94kJ \approx 58kJ`

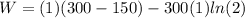
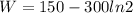
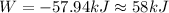
Therefore the work perfomed by this ideal carnot engine is 58kJ