Question

A body oscillates with simple harmonic motion along the x-axis. Its displacement varies with time according to the equation x = 5sin(pt + p/3). The phase (in rad) of the motion at t=2s is....?

Answer 1

To solve this problem we will use the general system of simple harmonic movement and compare this structure with the given value. From this equation we can find the phase. Our given value is

Data:

`x = 5 sin (\pi t + (\pi)/(3))`

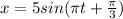
t = 2 s

The expression given from the theory for the harmonic movement is:

`x = A sin\theta`

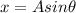
Where,

`\theta` = Phase Angle

A = Amplitude

Here the Phase angle is given as

`\theta = \omega t + \phi`

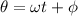
Comparing we have,

`\theta = \pi t + (\pi)/(3)`

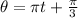
Replacing the time of t, we have that

`\theta = 2 \pi + (\pi)/(3)`

`\theta = (7\pi)/(3) rad`

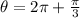
Therefore the phase of motion at t=2s is
`\theta = (7\pi)/(3) rad`