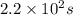Answer : The time taken by the reaction is
Explanation :
The expression used for second order kinetics is:
![kt=(1)/([A_t])-(1)/([A_o])](https://img.qammunity.org/2020/formulas/chemistry/college/431ujuvb5kogjm4uti8nh0187rr7wyxmp0.png)
where,
k = rate constant =
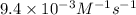
t = time = ?
![[A_t]](https://img.qammunity.org/2020/formulas/chemistry/college/wbj92t0z4axifcyqa24z3ary269op2iva8.png) = final concentration = 0.40 M
= final concentration = 0.40 M
![[A_o]](https://img.qammunity.org/2020/formulas/chemistry/high-school/38eb24kf04xqy5t88y9g0vzh3m04r4nqgg.png) = initial concentration = 2.16 M
= initial concentration = 2.16 M
Now put all the given values in the above expression, we get:
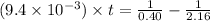
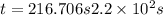
Therefore, the time taken by the reaction is