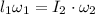Answer:2.17 rad/s
Step-by-step explanation:
Given
Each wheel has moment of inertia
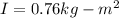
Linear speed speed
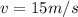
angular speed of tire
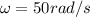
moment of inertia of motorcycle
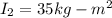
Initial moment of inertia

Due to absence of external Torque we can Conserve Angular Moment of inertia