Question

Water flows in a 6-m-wide rectangular channel with a depth of 0.55 m and a flow rate of 12 m3/s.

Determine the critical depth of the flow.

Express your answer in m.

Answer 1

`Y_(c)=0.7415m`

Step-by-step explanation:

General Formula for calculating the critical Depth is:

`Y_(c)=(V^(2) )/(g*A_(c)^(2))` Eq(1)

where:

V is the volume flow rate

g is gravitational acceleration i.e 9.81 m/s^2

A_c is the critical area

In case of Rectangular channel:

`A_(c) =w*y_(c)`

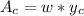
where:

w is the width

In case of Rectangular channel Eq (1) will become:

`Y_(c)=((V^(2) )/(g*w^(2) ) )^{(1)/(3) }`

`Y_(c)=((12^(2) )/(9.81*6^(2) ) )^{(1)/(3) }`

`Y_(c)=0.7415m`

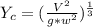
Actual depth i.e Y < Critical depth i.e Y_c

Flow is Supercritical