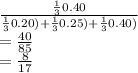Question

There are 3 boxes. First box contains 100 components of which 20 % are defective, second box contains 200 components of which 25 % are defective, third box contains 300 components of which 40 % are defective. Box is selected randomly and from this box one component is selected randomly. The chosen component turned out to be defective.

Determine the probability that it came from
a) second box.
b) third box.

Answer 1

Explanation:

Given that there are 3 boxes. First box contains 100 components of which 20 % are defective, second box contains 200 components of which 25 % are defective, third box contains 300 components of which 40 % are defective.

Box is selected randomly and from this box one component is selected randomly. The chosen component turned out to be defective.

Here A1, A2 and A3 events from drawing I, II and III box are mutually exclusive and exhaustive

B = The drawn ball is defective

Required probability

a) second box = P(A2/B)

=
`(P(A_2B))/(P(A_1B+P(A_2B+P(A_3B)`

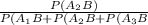
(by Bayes theorem of conditional probability)

=
`((1)/(3) 0.25)/((1)/(3) 0.20)+(1)/(3) 0.25)+(1)/(3) 0.40)) \\=(25)/(85) \\=(5)/(17)`

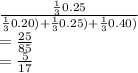
b) third box = P(A3/B)

=
`((1)/(3) 0.40)/((1)/(3) 0.20)+(1)/(3) 0.25)+(1)/(3) 0.40)) \\=(40)/(85) \\=(8)/(17)`